|
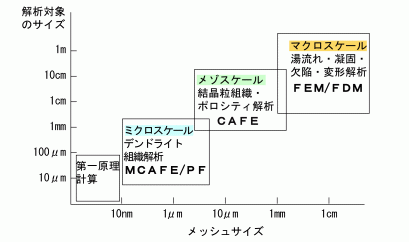
Computer Simulation of Micro,Macro Structures and Porosity in Castings by CAFE and MCAFE 鋳造工学 Vol.83(2011),No.8に掲載 1.はじめに 前回の連載講座の鋳物のポロシティ欠陥解析で紹介したように,鋳造シミュレーションの最初の目的はポロシティ欠陥を予測し, 如何にポロシティ欠陥の発生を抑えるかを対策することであった.そのために,多くのメッシュ作成や解析手法が開発されてきた.おそらく次の目的は 鋳物の結晶粒組織やミクロ組織を制御して最適の鋳物品質を得ることであろう.そのためには,従来から実施されているマクロ的な温度計算だけでは不十分であり, もっと桁違いの細かいメッシュを使用したミクロ解析が必要になる.そのためには,凝固基礎理論の発展も欠かせないものである.ここでは鋳物のミクロ, マクロ組織とポロシティ予測について紹介する. 2.マルチスケール鋳造シミュレーション 従来の鋳造シミュレーションは図1に示すマルチスケールという観点から見ると,マクロスケールの解析であり, これには湯流れ,凝固,欠陥,変形解析が含まれる.マクロスケールの解析手法については有限要素法(FEM)と直交差分法(FDM)がある. マクロスケールでのメッシュのサイズは1mmから数cmの範囲が一般的に使用されている.FDMでは個々のメッシュはさいころのような立方体であり, 作成されたメッシュモデルはさいころを積み重ねた形状になり,鋳物や鋳型の形状の近似精度は良くない.それに対してFEMでは有限要素法メッシュを 使用するので形状精度が良い.
メゾスケールの解析は数μmから1mm程度のサイズの直交メッシュ(CAメッシュ)を使用する.結晶粒組織やポロシティの定量予測を 行うことが可能でCA法またはCAFE法という手法を用いることが多い.両者の違いについては大きな差はないが,詳しく後に述べる. ミクロスケールの解析は,0.1μmから数μm程度のサイズの直交メッシュ(MCAメッシュ)を使用する. デンドライト組織やミクロポロシティの解析を行うことが可能である.MCAFE法とフェーズフィールド法(PF)の2種類の手法がある. フェーズフィールド法では1つのデンドライトのみを取り扱うことが多く,鋳物のように多くのデンドライトを同時に取り扱う必要がある場合には MCAFE法が適していると考えられる.MCAFE法については後に詳しく述べる. 図1には第一原理計算が記載されている.これは直接に鋳造シミュレーションを行なう技術ではないが,鋳造シミュレーションで 必要な多元系状態図や熱力学的パラメータを求める際に基礎となる解析手法であり,多元系合金を扱う鋳造シミュレーションでは重要な分野である. 鋳造の各工程のシミュレーションを図2に示す.(a)は保持炉から取鍋への注湯のマクロスケールシミュレーションである. 溶湯保持時や注湯時の温度変化を知ることが出来る.(b)は取鍋から鋳型への注湯のマクロスケールシミュレーションである.湯廻り不良,湯境欠陥, ガス巻き込み,湯流れパターン,注湯完了時の温度分布を知ることが出来る.(c)はメゾスケールの凝固時の結晶粒組織シミュレーションである. マクロ結晶粒組織を予測することが出来る.(d)はミクロスケールの凝固時のミクロ組織シミュレーションである.
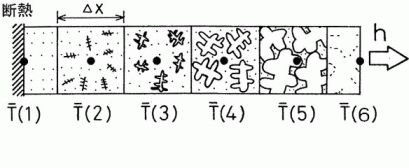
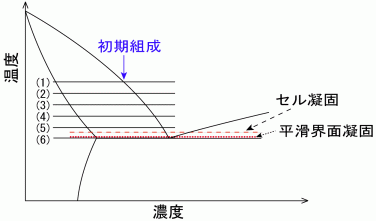
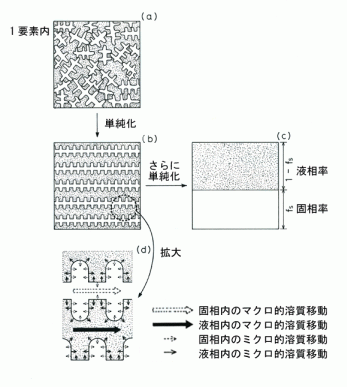
マクロスケールの解析とメゾスケール,ミクロスケールの解析を結び付けるには温度,固相率等をそれぞれのメッシュに 移し変えるだけでは不十分である.マクロ的熱移動と結晶粒・デンドライト成長を結び付ける理論が必要である. 1次元的なマクロ的熱移動とデンドライト成長を図3に模式的に示す.鋳物全体は6個の微小体積要素に分割されている.熱は右端から熱伝達率hで放出される. 冷却端の近くでは冷却が速いことより,デンドライトは冷却端に近いほど速く成長する.微小体積要素の平均温度は次式で表される. 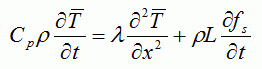 ・・・・・(2) ・・・・・(2)但し,Cpは比熱,λは熱伝導率,Lは潜熱,xは距離,tは時間である. 図3では,マクロスケールの6つの要素で(2)式の微分方程式を解くことによって要素の固相率が決まることを示した. 固相率が決まるということはマクロスケールの個々の要素内で図3にあるようにデンドライトが成長するということである.マクロスケールの要素内での デンドライトの成長のミクロスケールの解析について次章で説明する. 3. デンドライト凝固 従来の凝固シミュレーションのほとんどは鋳型及び鋳物内のマクロスケールの熱流のみを取り扱ったものである. しかしながら,ほとんどの鋳造プロセスでは複雑な3次元形状のデンドライトの成長によって凝固する.ここでは,マクロスケールの凝固解析とミクロスケールの デンドライト凝固解析を連成するための,デンドライト凝固解析法を紹介する1). 2元系共晶合金のデンドライト凝固の固液界面の温度変化の説明を図4に示す1). 図3の(1)〜(6)の要素に相当する温度を 図4の(1)から(6)の直線で示す.要素1は液相濃度は図4(1)に示すように初期組成であり,温度が初期組成での液相線温度である. 要素2から5は図4の(2)から(5)へ温度が低下すると共にデンドライトが成長する.要素6では残留液相が共晶組成になって凝固が完了する.
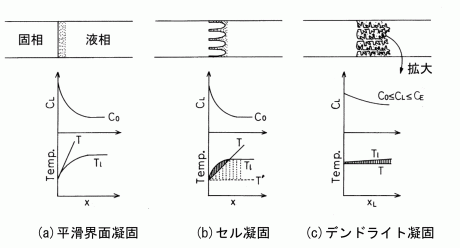
図5に3種類の凝固形態の固液界面での溶質濃度分布と温度分布を示す.デンドライト凝固では図4の(1)で液相温度になると初相が晶出し, (2)〜(6)の段階で温度が低下すると共にデンドライトが成長する.つまりデンドライトの固液界面の濃度が増大しながら凝固が進行する.要素内の温度勾配が 小さいために組成的過冷が大きくなり,組成的過冷を減少させるためにデンドライトが表面積を増大しながら成長する. 一方,温度勾配が大きい場合には固液界面の 溶質濃度は大きくなり,図5(a)のように平滑界面凝固になる.温度勾配が非常に大きく,凝固速度が小さくて平滑界面を保持出来れば図4の点線で示すように 共晶温度でほとんどの凝固が起こる.温度勾配がそこまでは大きくない場合にはセル凝固になり,図4の破線で示すように共晶温度よりも少し高い温度で凝固が起こる.
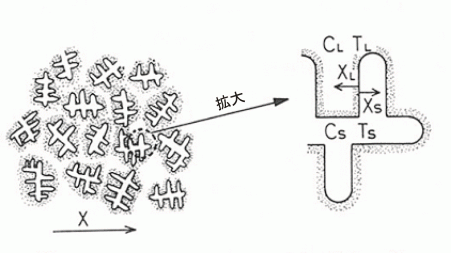
図6の左図に示すように,個々の微小体積要素内には幾つかのデンドライトセルが存在する.拡大した1つのデンドライトセルと記号の説明を 図6の右図に示す.固液共存域の液相と固相中の熱流には,図7に示すようにマクロ的及びミクロ的熱流がある.デンドライト表面で発生した凝固潜熱をできるだけ 速く固相または液相中に散逸させるために,ほとんどのミクロ的熱流はデンドライト表面に垂直になる.ミクロ的距離(図6のXL,XS)は 固液界面の法線方向に取る.
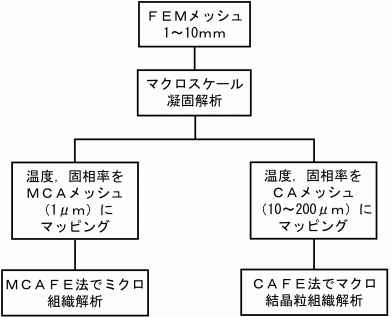
固液共存域の液相と固相のそれぞれの平均温度 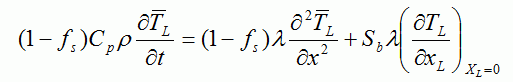 ・・・・・(3) ・・・・・(3)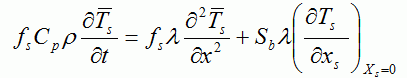 ・・・・・(4) ・・・・・(4)Sbはデンドライトの単位体積当りの比表面積である. 式(3)及び式(4)の左辺は,微小体積要素内の液相及び固相中に蓄積された全熱量である(図7(c)).これらの式の右辺第1項は, 液相及び固相中のマクロ的熱流によって蓄積された熱量である.右辺第2項は微小体積要素内のデンドライト表面から液相及び固相中に散逸する ミクロ的熱流の量である(図7(d)).式(3)及び式(4)の右辺第2項の合計は微小体積要素内で放出された潜熱量に等しいことより,次式が得られる. 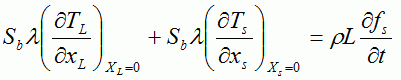 ・・・・・(5) ・・・・・(5)デンドライト成長におけるミクロ的熱流は3次元であるが,ここではマクロ的距離(X)とミクロ的距離(XL,XS)を 用いることによって,3次元性を考慮できる.また,ミクロスケールでの温度TL,Tsとマクロスケールでの固相率fsは(5)式で連成される. 液相内と固相内の物質移動は次のように表される. 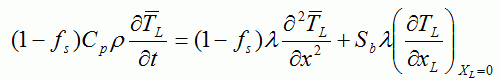 ・・・・・(6) ・・・・・(6)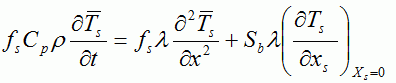 ・・・・・(7) ・・・・・(7)式(6)と式(7)の左辺は,微小体積要素内の液相と固相中に蓄積された溶質量を示す.微小体積要素内の拡散によるミクロ的な 物質移動のみを考え,微小体積要素同士のマクロ的な物質移動を無視すると,式(6)と式(7)の左辺の合計は0であり,次式が得られる. 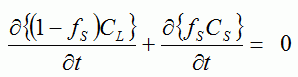 ・・・・・(8) ・・・・・(8)式(6)と式(7)の右辺第一項は固相率変化による溶質の蓄積量である.第2項は微小体積要素内のデンドライト表面で排出された 溶質の液相内および固相内へ拡散するミクロ的な物質流による溶質蓄積量である.式(6)と式(7)を式(8)に代入すると次式のように固液界面での物質移動が表される. 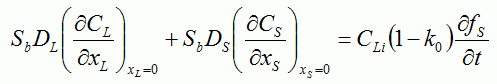 ・・・・・(9) ・・・・・(9)ミクロスケールでの濃度CL,Csとマクロスケールでの固相率fsは(9)式で連成される.ここで,(5)式と (9)式を整理して比較すると,ミクロ組織解析用のメッシュ(MCAメッシュ)内で温度勾配は濃度勾配よりずっと小さいため,MCAメッシュ内では温度一定と 仮定して良いことが分かる1). また,MCAメッシュ内のΔT(全過冷度)はΔTk(動的過冷度),ΔTD(拡散による過冷度), ΔTr(曲率による過冷度)の和として求める. 以上は,マクロスケール解析とミクロスケール解析の連成の仕方について述べた.具体的には図8に示すように,FEMメッシュを使用して マクロスケール凝固解析を行い,10〜200μm程度CAメッシュに温度と固相率をマッピングして,これをマクロスケールで得られたマクロ的な熱流の条件として, 後はCAFE法の理論でメゾスケールのマクロ結晶粒組織解析を行う.ミクロスケールの解析については,1μm程度の細かいMCAメッシュに温度と固相率をマッピングして, これをマクロスケールで得られたマクロ的な熱流の条件として,後はMCAFE法の理論でミクロ組織解析を行う.
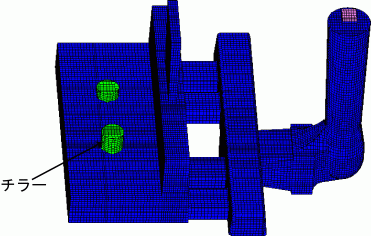
4. メゾスケール結晶粒組織解析 鋳物の結晶組織予測についてはRappazら2)3) がCA法(セルラー・オートマトン法)を発表し,その後国内でも,Choら4), 中間5),大平ら6)によって研究された. CAFE法という呼び方はGandinら3)によってCellular Automaton Finite Element の略として使われたのが最初であろう. マクロスケールでは鋳物形状をFEMメッシュで正確に表し,メゾスケールでは100μm程度以下の細かい直交メッシュ(CAメッシュ)を用いてCA法で解析するという手法である. メゾスケールのCAFE法の解析は,マクロスケール解析で得られた温度変化,ポロシティ量,サイズ,数をCAメッシュにマッピングして, 以下の述べるような方法でマクロ結晶粒組織とポロシティ空洞の予測を行うことが出来る. 図9にチラーを使用した平板鋳物のFEMメッシュモデルを示す8) .鋳物はAC4C合金で鋳型はけい砂を使用した減圧造型鋳型である. これを例として,CAFE法による解析方法を説明する.
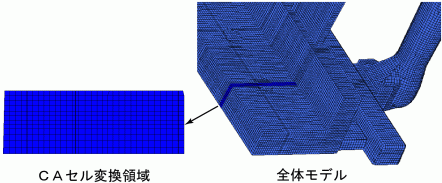
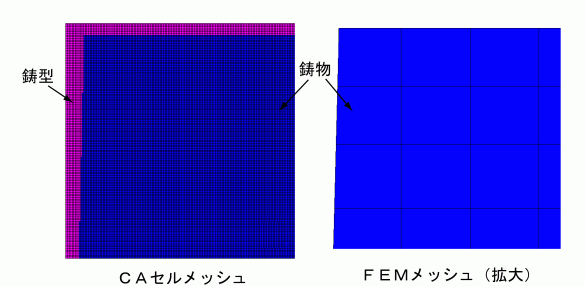
(1)FEMメッシュによるマクロスケールの湯流れ,凝固解析 数mmサイズのFEMメッシュを使用して湯流れ,凝固解析を行う.得られた平均温度,平均固相率をタイムステップ毎に全要素について保存しておく. (2)CAセル分割 鋳物のサイズが小さい場合はマクロスケールのFEM全体をそのままCAセルにメッシュ分割する.しかし,多くのの場合は必要なメモリが大き過ぎたり, 計算時間がかかり過ぎることがある.このような場合には,図10に示すように全体モデルの一部をCAセルモデルに変換する.図10のCAセル変換領域の左上の部分での CAセルメッシュとFEMメッシュの比較を図11に示す.CAセルメッシュは鋳物ではない要素は鋳型に設定される.FEMメッシュの左側面は少し傾斜しているが, 有限要素法メッシュを使用していることより正確に形状を近似できている.CAセルメッシュは直交メッシュであるために左側面は少し形状近似精度が劣るが, メッシュが細かいのであまり精度が悪くならない.
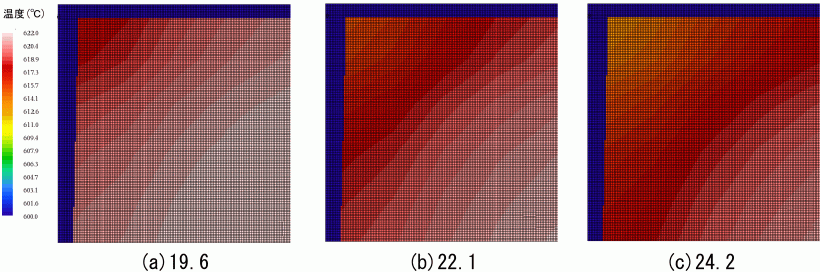
(3)温度,固相率データの変換 FEMメッシュからCAセルメッシュへマッピングされた温度分布の一例を図12に示す.
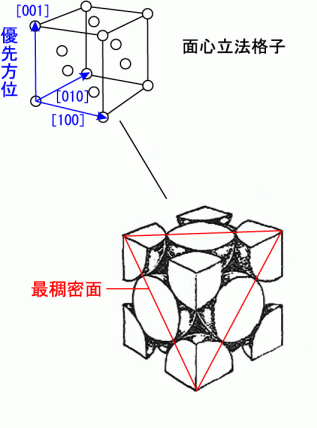
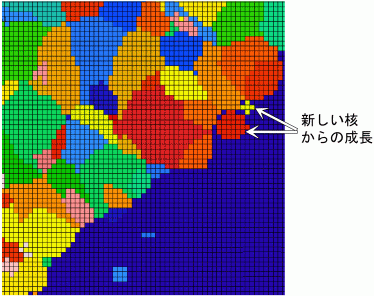
(4)核生成 液相中で固相が晶出するのは固相の核生成から始まる.次式のようなガウス分布曲線によって不均質核生成が起こると仮定する5)9). 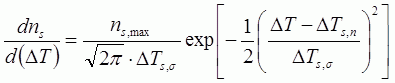 ・・・・・(13) ・・・・・(13)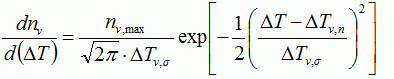 ・・・・・(14) ・・・・・(14)但し,ns =鋳物表面での結晶粒の密度 nv =鋳物内部での結晶粒の密度 ns,max =鋳物表面最大核発生密度 nv,max =鋳物内部最大核発生密度 ΔTs,n =鋳物表面核生成平均過冷度 ΔTv,n =鋳物内部核生成平均過冷度 ΔTs,σ =鋳物表面核生成過冷度偏差 ΔTv,σ =鋳物内部核生成過冷度偏差 タイムステップ毎に液相セルに乱数を発生させる.その値が内部の液相セルで(14)式で示される値よりも小さい場合には, 図13に示すように,濃い灰色の液相セルが薄い灰色の固相に変化する.表面の液相セルでは(13)式で示される値以上であればセルは固相になる. 一般には鋳物表面のほうが内部より核が発生し易いので,(14)式より(13)のほうが結晶粒の密度が大きくなるように上記8つのパラメータが設定されている. また,ここで発生した結晶粒の結晶方位は乱数によってランダムに決まる. (5)デンドライト成長方位 金属が液相から固相に成長する際の固液界面は最稠密面になることが表面自由エネルギーが最小になるので有利である. 図14に面心立方格子の場合を示すが,最稠密面は(111)である.デンドライト表面は(111)で最も安定であり,表面をこの面に保ったままで, 稜線に沿って成長するのが最も安定である.このように,デンドライトの優先方位は稜線方向の[001], [100],[010]である. 優先方位に近いデンドライトは成長速度が速くなる.
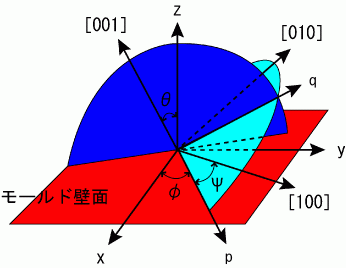
3次元のCA法でデンドライト成長方位の考慮の方法について詳しく述べた報告は少ない.中間4) ,Changら10), Zhuら7) は図15に示すようなオイラー角を用いて3次元の結晶方位を考慮した.メッシュの座標系(x,y,z)のモールド壁面をx,y軸を含む面とする. 核生成した結晶の優先方位を図中に[001], [100],[010]で示した.デンドライトの優先方位は90度回転対称である.図15で定義される3つのオイラー角θ,φ,ψによって 結晶粒の優先方位とメッシュの座標系のずれが決まる.
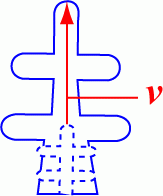
(6)デンドライト成長速度 デンドライトは図16に示すように,1次及び2次の枝がデンドライトの軸に沿って成長する.その成長 速度νはKGT理論11) によって導出され,次式の形式で過冷度ΔTの関数としてCA法で計算されることが多い4)5)12). 上式中の係数a2,a3は合金の種類によって決まる.過冷度ΔTは液相線温度とCAメッシュに マッピングされた温度の差を用いる.i要素のタイムステップΔtの間に成長する長さliは次式のように表される. ここで,Wiは結晶粒の優先方位とメッシュの座標系のずれの補正係数であり図15のオイラー角を用いた座標変換で求まる. (7)結晶粒方位の決定 液相CAセルの結晶方位の決定方法について図17に示す.この図は2次元表示であるので,1つの四角のセルには辺で接している要素が4個と, 点で接している要素が4個あり,合計8個の隣接要素がある.これが3次元になると隣接要素は26個になる.結晶方位は次のような方法で決まる.Δt毎に, 注目している液相セルについて,26個の隣接セルのうち固相であるセルのみを考える.Δt以内に最も早く注目している液相セルに到達する固相セルがあれば, この固相と同じ結晶方位の固相に変態する.全ての液相セルについてΔt毎にこの判定を行なう.到達する距離と速さは(16)式で計算する. これを繰り返すと,図18に示すように,マクロ結晶粒組織が形成される.図19は結晶方位の表示色を変更しメッシュのラインを消して表示したものである.
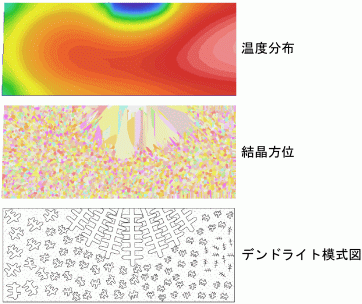
図10の平板鋳物のマクロ結晶粒組織の実験結果と解析結果との比較を図20に示す.中央上部にチラーを設置してあったので, その下が柱状晶組織,残りは等軸晶組織であった.実験と解析は比較的良く一致している.図20の場合は41sで結晶方位が決定されたが,この時点での 結晶方位と温度分布を図21に示す.この図で,結晶方位は41sで確定しているが,温度分布から固相率を算出してデンドライト組織を模式的に書いたのが一番下の図である. 固相率としては,まだ20%程度しか凝固は進んでいないが,デンドライトの網状組織によってこの時点で鋳物全体のマクロ結晶粒組織が確定している. これ以降は方位の決まった結晶粒内でデンドライト間の液相が固相に変態して凝固が完了することになる.
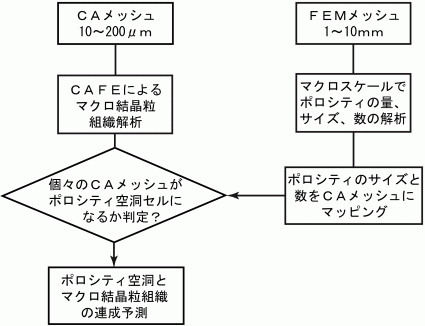
CAFE法ではマクロ結晶粒組織の他に,ポロシティ予測も可能になっている.図22にCAFE法によるポロシティ予測のフローチャートを示す. まず,FEMメッシュを作成し,マクロスケールで凝固解析及びポロシティ解析13) を行うことによって,ポロシティの量,サイズ,数を求める. 一方,メゾスケールとしてはFEMメッシュからCAメッシュを作成する.CAFE法によって各CAセルが結晶粒方位が決まった後でも,ポロシティ空洞になる場合には 固相セルから空洞セルに変更する.この際はマクロスケール解析で得られたポロシティのサイズと数をCAメッシュにマッピングした値を利用して確率的に決定する. このようにして,メゾスケールのポロシティ空洞とマクロ結晶粒組織の予測が可能である14). 前回の講座で紹介したメゾスケールシミュレーションによって得られたAC4CH合金コニカルモールドのマクロ結晶粒組織とポロシティを図23に示す. 解析結果は粟野15)の実験結果と良く一致している.ポロシティが分布図でなく,200μmのCAメッシュによって空洞セルか固相セルかの区別がつき具体的に表示できる.
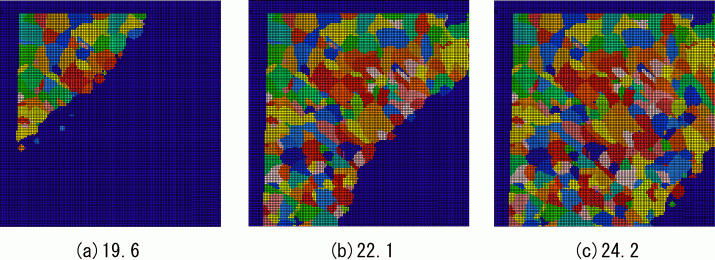
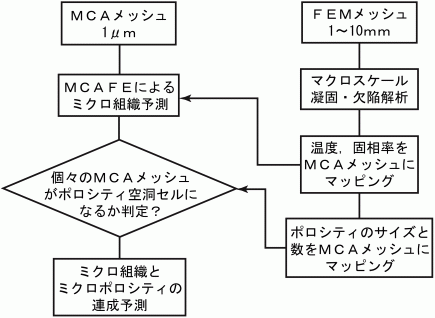
5.ミクロスケール鋳造組織解析 ミクロスケールでのデンドライト組織の解析はフェーズフィールド法という手法が一般的であり大学関係で多くの研究が行われている. フェーズフィールド法は1つのデンドライトのみを解析し,核生成を考慮した複数のデンドライトを解析することは難しい.鋳物のミクロ組織を知るには, 核生成を考慮した多数のデンドライトの同時成長を解析できることが重要である.ここではMCAFE法によるミクロスケールのミクロ組織予測について紹介する. MCA法はZhuらによってCA法を用いてミクロ組織を予測する場合に使われたのが最初であろう12) 17) .MCAはModified Cellular Automatonの 略として使用された.マクロスケールのFEMメッシュで全体の形状を精度良く近似してミクロスケール解析を行うということでMiroscale Cellular Automaton Finite Elementの 略としてMCAFE法19) と呼んでいる.福岡ら18)もMCA法でAl-Si合金のミクロ組織解析を報告している. MCAFE法によるミクロ組織及びミクロポロシティ予測のフローチャートを図24に示す.計算に使用するメッシュは1μm程度の直交メッシュ(MCAメッシュ)である. マクロスケール凝固,欠陥解析で求められた温度,固相率,ポロシティサイズ,数をミクロスケールのMCAメッシュにマッピングすることによってマクロ的な熱流と ポロシティ発生の条件として解析する.このようにしてマクロスケールとミクロスケールの連成計算が可能になっている.個々のMCAメッシュの固相への核生成と デンドライト成長については,メゾスケールのCAFE法と同様に取り扱う.ミクロスケールでの温度,濃度,固相率については3章で述べた基礎式を使用する. 図23のAC4CH合金コニカルモールドのミクロスケールシミュレーションによって得られたデンドライトの成長過程を図25に示す. (a)58sで細かいα相デンドライト組織で成長しており,(b)70sではα相デンドライトの成長が進み,(c)73sではSi相が2次デンドライトアーム間や デンドライト間に晶出し始める.(d)77sでは最終凝固のデンドライト間にSi相が晶出して凝固が完了する.(a)から(d)の中央右下の同じ位置に楕円が書かれている. (a)では楕円の中に10個の2次デンドライトアームがあるが,(b)では7個に減少し,(c)と(d)では6個に減少している.デンドライト凝固時に2次デンドライトの 数が減少することは“Coarsening”と呼ばれており,Kattamisら16)によって実験的にも理論的にも明らかにされてきた. MCAFE法による解析でもこのように“Coarsening”を再現できることが分かる.
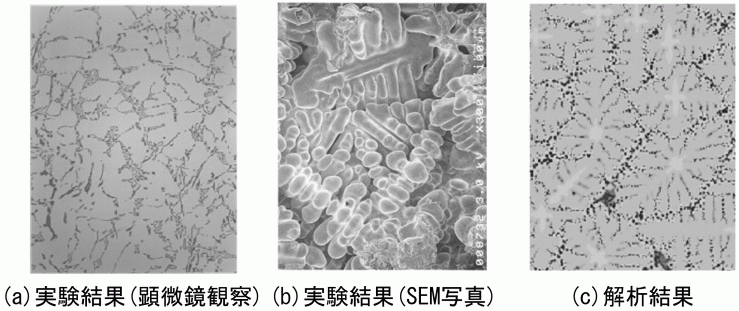
デンドライト組織の解析結果と実験結果の比較を図26に示す.デンドライト間にSi相が現れ,全体的に実験結果と比較的良く一致している. 但し,実験結果では3次元的に成長した様子が見えるのに対し,解析は2次元で解析しているので平面的である.つまり,平面上に核が発生し, 平面内でのみ成長することが原因である.3次元でも図15に示すオイラー角の取り扱いをしているので解析は可能であるがメモリ容量と計算時間の関係で 2次元解析になってしまうことが多い.図25の解析は1mmの四角の領域を1μmのMCAメッシュで分割しており,要素数は100万個であるが, 1mm立方体にすると10億個にもなってしまう.問題は,計算のメモリと計算速度であるので,今後解決されていくと考える.
6.まとめ 鋳物のミクロ,マクロ,ポロシティ組織予測について,次のようにまとめられる. 文献 1) 久保公雄:日本金属学会誌 54(1990) 8162) M.Rappaz, Ch.-A.Gandin : Acta Metall. Mater. 41 (1993) 345 3) Ch-A.Gandin, J.-L.Desbiolles, M.Rappaz, Ph.Thevoz : Metall. Mater. Trans. B (1999) 3151 4) 中間敦司:日立金属技法14 (1998) 81 5) Sang-hyun Cho, 岡根利光,梅田高照:鋳物 71 (1999) 246 6) 大平竜也,鵜飼修,桂木一行,下畑幸郎,Sang hyun Cho, 梅田高照:日本機械学会論文集(B編)68 (2002) 819 7) M.F.Zhu, C.P.Hong : ISIJ Int. 42 (2002) 520 8) 久保公雄,富田剛利:第149回全国講演大会講演概要集(2006) 88 9) Ph.Thevoz, J.L.Desbiolles, M.Rappaz : Metall. Trans. 20A (1989) 311 10) Y.H.Chang, S.M.Lee, K.Y.Lee, C.P.Hong : ISIJ Int. 38 (2002) 63 11) W.Kurz, B.Giovanola, R.Trivedi : Acta Metall. 34 (1986) 823 12) M.F.Zhu, C.P.Hong : ISIJ Int. 41 (2001) 436 13) K.Kubo, R.D.Pehlke : Metall. Trans. 16B (1985) 359 14) 久保公雄,出来尚隆,佃公博:第153回全国講演大会講演概要集(2008) 74 15) 粟野洋司:軽金属56 (2006) 335 16) T.Z.Kattamis, J.C.Coughlin, M.C.Flemings : Trans. TMS-AIME 239 (1985) 1504 17) M.F.Zhu, J.M.Kim, C.P.Hong : ISIJ Int. 41 (2001) 992 18) 福岡仁,Sang-Hyun Cho, Jeong-Kil Choi, 鈴木俊夫:鋳造工学74(2002) 638 19) 久保公雄:第147回日本金属学会講演概要(2010) 165 |